
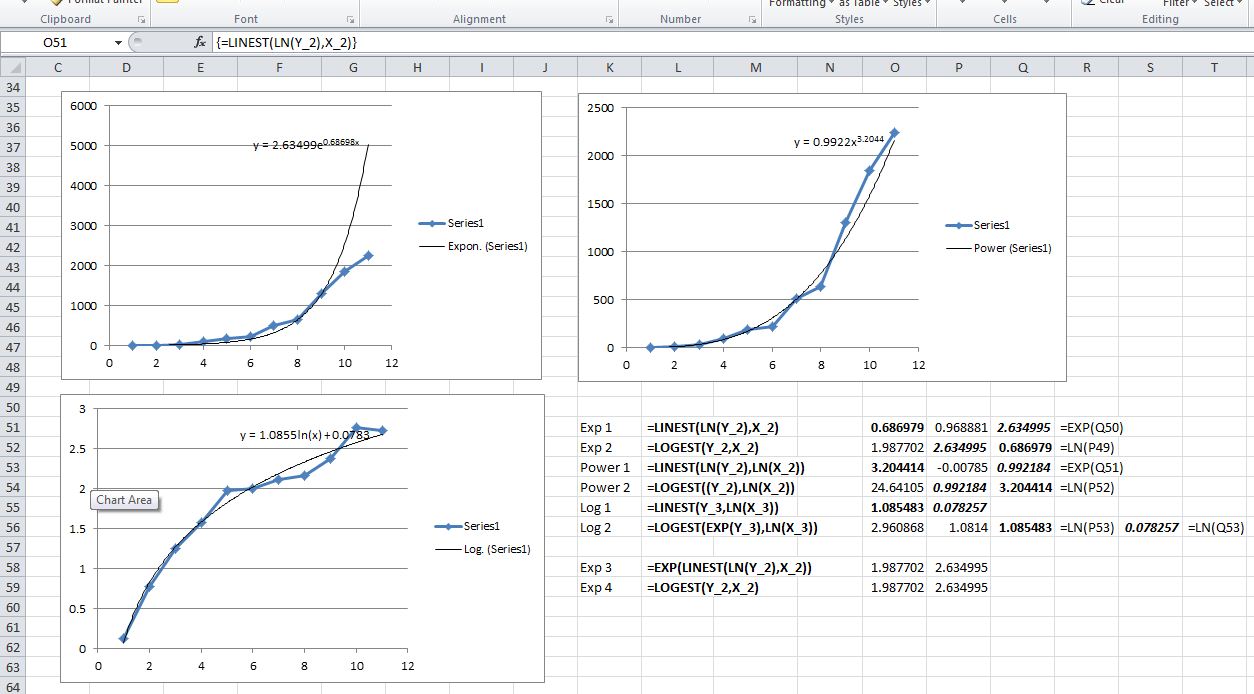
Īn advantage to using LINEST to get the coefficients that define the polynomial equation is that we can return the coefficients directly to cells. For a polynomial equation, we do that by using array constants. flow rate through a water valve, and after plotting the data on a chart and trying different trendlines we see that the data is quadratic, as in the example above.Įven though this data is nonlinear, the LINEST function can also be used here to find the best fit curve for this data. Let’s say we have some experimental data of pressure drop vs. TRUE will return the statistics and FALSE will return no statistics. stats (optional) is an argument that tells whether to return regression statistics.
However, there is an option that provides a robust way to curve fit in Excel using the LINEST function. This can cause problems if the data is updated, and the coefficients are not updated in the spreadsheets. This will make any formula that uses these coefficients only accurate to the same number of significant digits.Īlso, there is no way to reference the coefficients of the equation in the spreadsheet without manually typing them into cells. In some cases, it may provide only 1 or 2 significant digits for the equation coefficients.
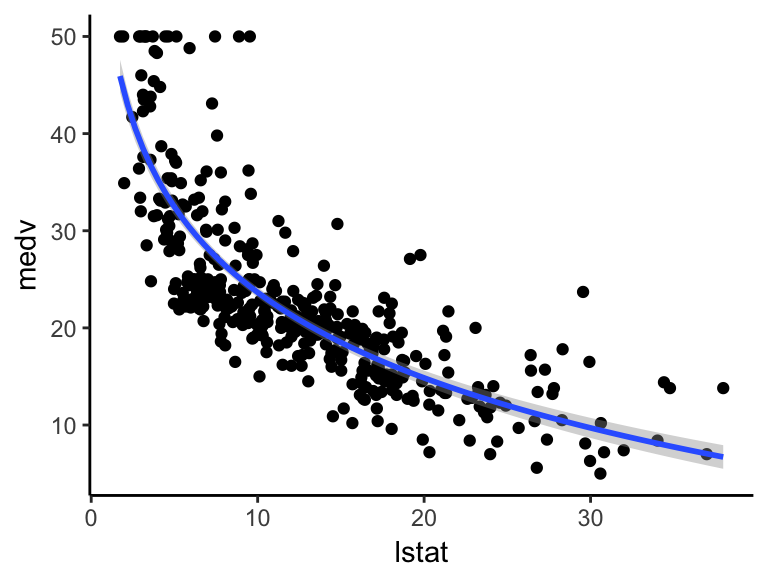
That means the polynomial equation fits the data better.Īlthough the trendline option is convenient, it may not always be the best option when you want to know the equation that best fits the data. However, a second-order polynomial fits the data with an R-squared value of 0.998. From the image below, we can also clearly see that it is not a good fit. Try different types of curves to see which one maximizes the value of R-squared.įor this data set, a logarithmic equation fits the curve with an R-squared value of 0.7992. In the Format Trendline pane, select the options to Display Equation on chart and Display R-Squared value on chart. Then right click on the data series and select “Add Trendline …”


 0 kommentar(er)
0 kommentar(er)
